Federated Learning

, ,

Hello there! Have you ever wondered if it’s possible to train a high-performing machine learning model without scraping every last bit of data into a single repository? Luckily, federated learning (FL) provides a method for doing exactly that—and, as several researchers continue to uncover, there’s a wealth of techniques to bolster its security. In this post, we’ll explore federated learning’s fundamentals, discuss advanced aggregation methods, delve into privacy solutions like differential privacy, and introduce cryptographic approaches such as homomorphic encryption. To keep things firmly on the technical side, we’ll walk through some mathematics and illustrative Python snippets. This post is inspired by insights from my own bachelor thesis research at this GitHub repository and thesis.

Introduction to Federated Learning

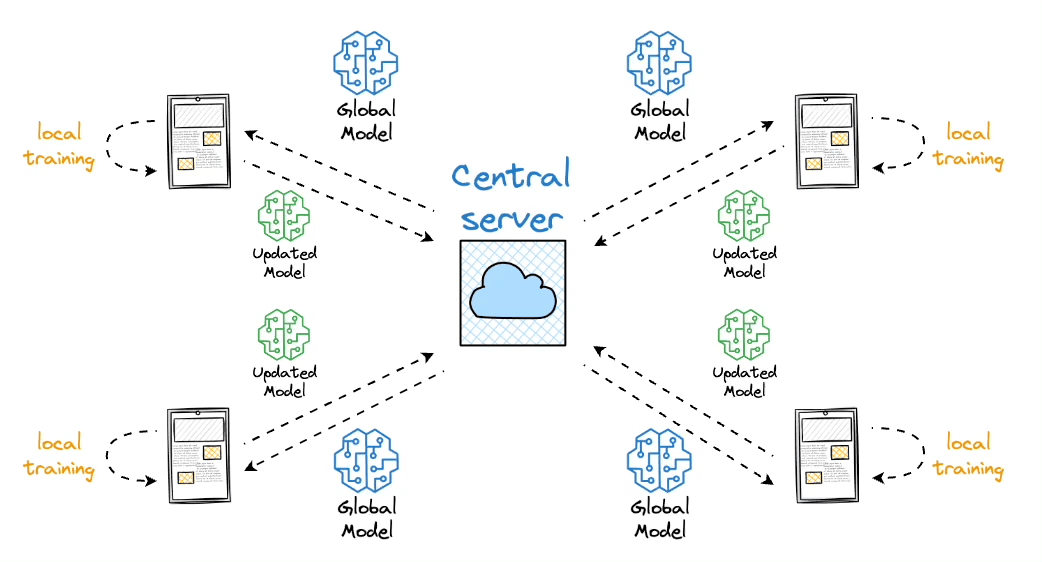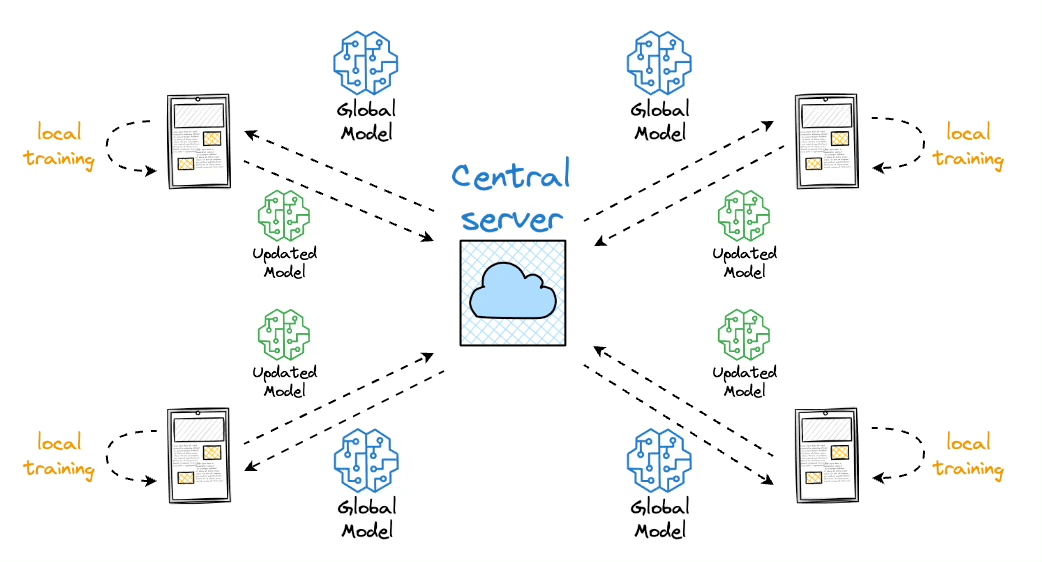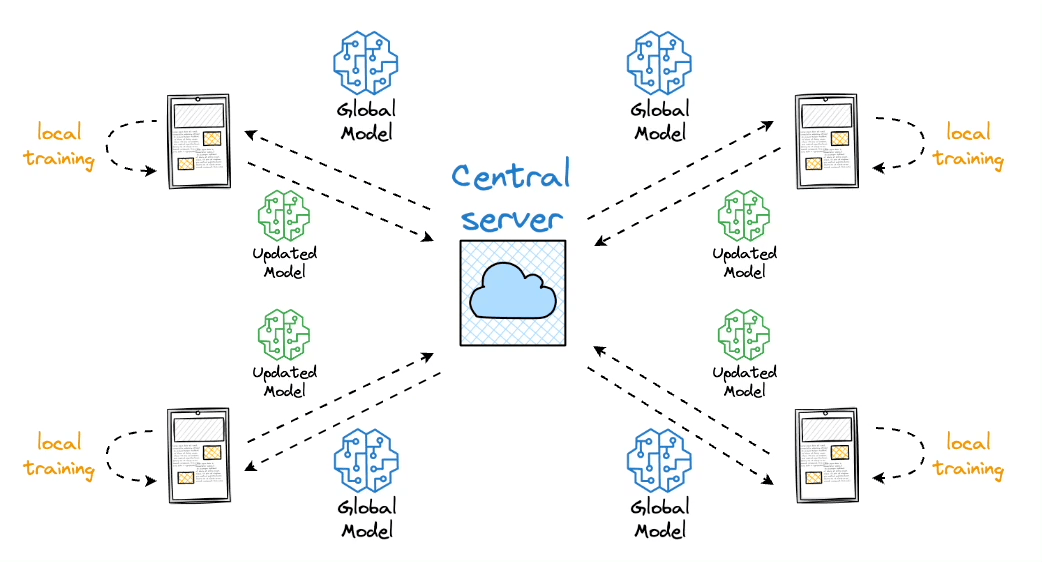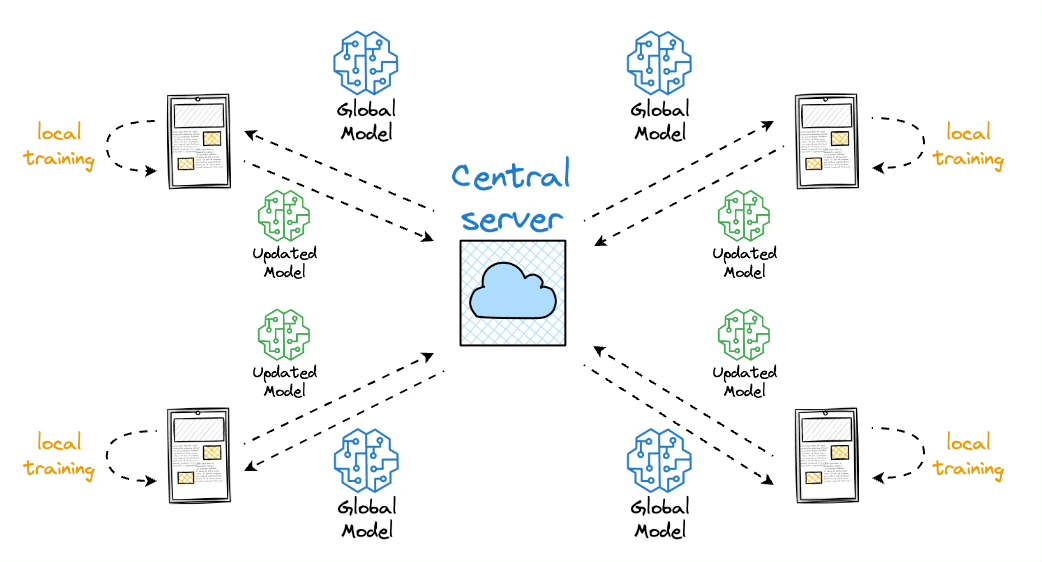
In traditional machine learning, a centralized server aggregates data from multiple sources and trains a single global model. By contrast, federated learning pushes the model to where the data physically resides. Each device (or client) has its own local dataset, trains on that data, and sends carefully curated updates (rather than raw data) to a central location for aggregation.

Mathematically, suppose we have a global minimization problem:

$$\min_{w\in\mathbb{R}^d} F(w),$$

with

$$F(w) = \frac{1}{N}\sum_{i=1}^N \ell(x_i, y_i; w),$$

where $\ell$ is a loss function, $x_i$ the local training samples, $y_i$ their labels, and $w$ the model parameters. If we distribute the data across $K$ clients, we may define:

$$F(w) = \sum_{k=1}^K \frac{n_k}{n_{total}} F_k(w),$$

where $F_k$ denotes the local loss for client $k$, $n_k$ is the number of samples on client $k$, and $n_{total} = \sum_{k=1}^K n_k$.

In federated learning:

  1. Client devices download the current global model $w^t$
  2. They each run local training (e.g., minibatch SGD) for a few epochs to refine $w^t$
  3. They send their updated parameters $\Delta w_k^t$ (or the entire updated model $w_k^t$) back
  4. The server aggregates these updates to produce a new global model $w^{t+1}$

This decentralized method significantly reduces data transfer and opens up new possibilities for making it safer still.

A Quick Look at Classic Federated Aggregation

FedSGD

FedSGD is one of the earliest approaches. It performs a single step of gradient descent on each client and aggregates all gradients:

$$w^{t+1} = w^t - \eta \sum_{k=1}^K \frac{n_k}{n_{total}} \nabla F_k(w^t),$$

where η is the learning rate. It’s communication-heavy because every client has to send its gradient on each round t.

FedAvg

By far the most popular aggregator is FedAvg - let each client train locally for $E$ epochs before sending updates. Then:

$$w^{t+1} = \sum_{k=1}^K \frac{n_k}{n_{total}} w_k^t,$$

where $w_k^t$ is the locally trained model on client $k$. FedAvg can drastically reduce the communication rounds and training time, while typically preserving performance - though it is more sensitive to the non-IID nature of real-world data.

Beyond the Arithmetic Mean: Robust Aggregation

A known risk in federated learning is that malicious or buggy clients can send “poisoned” updates. The standard arithmetic mean aggregator (e.g., FedAvg) is not robust to outliers. One proposed solution is the geometric median approach, sometimes called Robust Federated Aggregation (RFA).

Geometric Median Formulation

Let ${w_1,\ldots,w_m}$ be the client updates to be aggregated. The geometric median $z \in \mathbb{R}^d$ minimizes:

$$\min_z \sum_{k=1}^m \alpha_k ||w_k - z||,$$

where $\alpha_k$ are weights (often $\alpha_k = \frac{1}{m}$). In practice, we approximate $z$ iteratively (e.g., via a Weiszfeld algorithm):

$$z^{(i+1)} = \frac{\sum_{k=1}^m \beta_k^{(i)} w_k}{\sum_{k=1}^m \beta_k^{(i)}}, \text{ where } \beta_k^{(i)} = \frac{\alpha_k}{\max{\nu, ||w_k - z^{(i)}||}}.$$

After a few iterations, outlier updates get “down-weighted.”

Making Updates Private: Differential Privacy

Even if clients share only gradients, an adversary or a curious server might reconstruct private data by closely analyzing these updates. Differential privacy (DP) defends against such inference attacks by systematically adding noise.

Core Definition

A randomized mechanism $\mathcal{M}$ is $(\epsilon,\delta)$-differentially private if for any two neighboring datasets $D$ and $D’$ (differing in exactly one record),

$$\Pr(\mathcal{M}(D) \in S) \leq e^\epsilon \Pr(\mathcal{M}(D’) \in S) + \delta,$$

for all measurable subsets $S$. Intuitively, flipping just one person’s data in or out shouldn’t change the probability distribution of outputs too much.

Applying DP to Federated Averaging

In DP-FedAvg, each client clips its gradient to a certain $\ell_2$-norm bound $C$ and then adds noise before sending it:

  1. Clip:
    $$\tilde{g}_k = \frac{g_k}{\max(1, \frac{||g_k||_2}{C})},$$
    ensuring $||\tilde{g}_k||_2 \leq C$.

  2. Add noise:
    $$\hat{g}_k = \tilde{g}_k + \mathcal{N}(0, \sigma^2C^2\mathbf{I}),$$
    where $\sigma$ is chosen according to a privacy budget $\epsilon$.

The updates are now noised, making data reconstruction from a single client extremely difficult.

A (Very) Short Python Prototype

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np

def dp_clip_and_noise(
    grad: np.ndarray,
    clip_norm: float = 1.0,
    noise_multiplier: float = 1.0
) -> np.ndarray:
    """
    Clips and adds Gaussian noise to a gradient tensor for differential privacy.
    
    Args:
        grad: np.array representing the local gradient
        clip_norm: Max allowed L2 norm for the gradient
        noise_multiplier: Scales the noise relative to clip_norm
    
    Returns:
        np.ndarray: Anonymized gradient
    """
    # Clip
    norm = np.linalg.norm(grad)
    if norm > clip_norm:
        grad = (grad / norm) * clip_norm
    
    # Noise
    noise_std = noise_multiplier * clip_norm
    noise = np.random.normal(loc=0.0, scale=noise_std, size=grad.shape)
    
    return grad + noise

In a real FL pipeline, each client applies dp_clip_and_noise(...) to its local gradient, ensuring the global aggregator only sees a “blurred” view.

Hiding Model Updates via Homomorphic Encryption

While differential privacy focuses on bounding the server’s ability to deduce individual training records, homomorphic encryption (HE) ensures the server can only see encrypted data throughout the training process.

What is Homomorphic Encryption?

A fully homomorphic encryption scheme $\mathcal{E}$ supports certain arithmetic operations on ciphertexts — often additions and multiplications — without decrypting them. Concretely, if $Enc$ is the encryption function, you can compute:

$$Enc(a) \oplus Enc(b) = Enc(a * b),$$

where $\oplus$ and $*$ refer to either addition or multiplication in the chosen scheme. This securely allows an aggregator node to sum gradients from multiple clients, while never seeing them in plaintext.

Homomorphic Aggregation Example

  1. Each client encrypts its update:

    $$c_k = Enc(w_k),$$

    for $k = 1,\ldots,K$

  2. The server sums the ciphertexts:

    $$c_{sum} = \sum_{k=1}^K c_k,$$

    using homomorphic addition.

  3. An entity with the private key can decrypt:

    $$Dec(c_{sum}) = \sum_{k=1}^K w_k.$$

Either the clients themselves collectively decrypt (via multi-party computations) or a trusted aggregator does.

Below is a conceptual snippet (non-functional “pseudocode” style for brevity, since production-level HE libraries can be quite specialized):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
from typing import Any, Protocol

class HEContext(Protocol):
    """Protocol defining required methods for homomorphic encryption context"""
    def encrypt_zeros(self) -> Any: ...
    def homomorphic_add(self, a: Any, b: Any) -> Any: ...
    def decrypt(self, ciphertext: Any) -> Any: ...

def homomorphic_aggregate(
    encrypted_updates: list[Any], 
    he_context: HEContext
) -> Any:
    """
    Securely aggregates a list of encrypted updates using homomorphic addition.
    
    Args:
        encrypted_updates: List of encrypted model updates (ciphertexts)
        he_context: Context object providing homomorphic encryption operations
    
    Returns:
        Any: Single ciphertext representing the homomorphically summed updates
    """
    # Start with a ciphertext 'zero' in the correct scheme
    c_sum = he_context.encrypt_zeros()
    for c_u in encrypted_updates:
        # Homomorphic addition
        c_sum = he_context.homomorphic_add(c_sum, c_u)
    return c_sum

def decrypt_sum(c_sum: Any, he_context: HEContext) -> Any:
    """
    Decrypt the aggregated ciphertext to get the sum of plaintext updates.
    
    Args:
        c_sum: Encrypted sum of model updates
        he_context: Context object providing homomorphic encryption operations
        
    Returns:
        Any: Decrypted sum of the original plaintext updates
    """
    return he_context.decrypt(c_sum)

In practice, you might combine this approach with differential privacy for an extra privacy buffer, or with robust aggregators to guard against malicious participants.

Putting It All Together

Workflow Recap

  1. Distribute Model: The server (or coordinator) sends the current model to available clients.
  2. Local Updates: Each client trains on its private data.
  3. Secure Aggregation via
    • Robust aggregator (geometric median or other outlier-resistant method).
    • Differential privacy (clip gradients, inject noise).
    • Homomorphic encryption (server only sees ciphertexts).
  4. Global Model Update: Decrypt (if needed), or combine noised gradients to produce a new $w^{t+1}$.
  5. Repeat until convergence or resource limits.

Practical Considerations

  • Non-IID Data: FL typically deals with data that’s not independent and identically distributed. In extreme cases, robust methods like geometric median can help mitigate drastically different updates.
  • Client Dropout: Real cross-device FL sees clients go offline frequently, so the aggregator must handle partial participation.
  • Performance Overhead: Differential privacy introduces accuracy drops if noise is large; homomorphic encryption can be computationally expensive. Balancing security vs. performance is key.

Example: Federated Training Loop in Python

Below is a condensed code snippet showing a theoretical loop. It uses:

  1. local_train() to do local SGD,
  2. dp_clip_and_noise() for differential privacy,
  3. np.mean() as a placeholder aggregator (though you could switch it for a robust aggregator function or a homomorphic one).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np

def local_train(
    model_params: np.ndarray[np.float64], 
    local_data: tuple[np.ndarray[np.float64], np.ndarray[np.float64]], 
    epochs: int = 1, 
    lr: float = 0.01
) -> np.ndarray[np.float64]:
    """
    Train model parameters using gradient descent on local data.
    
    Args:
        model_params: Initial model parameters as numpy array
        local_data: Tuple of (X, y) arrays containing features and labels
        epochs: Number of training epochs
        lr: Learning rate for gradient descent
        
    Returns:
        np.ndarray: Updated model parameters as numpy array
    """
    w = np.copy(model_params)
    for _ in range(epochs):
        grad = compute_gradient(w, local_data)
        w = w - lr * grad
    return w

def compute_gradient(
    w: np.ndarray[np.float64], 
    data: tuple[np.ndarray[np.float64], np.ndarray[np.float64]]
) -> np.ndarray[np.float64]:
    """
    Compute gradient of MSE loss for linear regression.
    
    Args:
        w: Model parameters of shape (dim,)
        data: tuple of (X, y) where X has shape (num_samples, dim) 
             and y has shape (num_samples,)
             
    Returns:
        np.ndarray: Gradient vector of same shape as w
    """
    X, y = data
    preds = X @ w
    errs = preds - y
    grad = (X.T @ errs) / len(X)
    return grad

def federated_round(
    global_params: np.ndarray[np.float64],
    clients_data: list[tuple[np.ndarray[np.float64], np.ndarray[np.float64]]],
    clip_norm: float,
    noise_multiplier: float
) -> np.ndarray[np.float64]:
    """
    Execute one round of federated training with differential privacy.
    
    Args:
        global_params: Current global model parameters
        clients_data: list of (X, y) data tuples for each client
        clip_norm: L2 norm threshold for gradient clipping
        noise_multiplier: Scale of Gaussian noise for differential privacy
        
    Returns:
        np.ndarray: Updated global parameters after aggregating client updates
    """
    updated_params = []
    for local_data in clients_data:
        w_k = local_train(global_params, local_data)
        grad_k = w_k - global_params  # approximate local gradient
        grad_k_dp = dp_clip_and_noise(grad_k, clip_norm, noise_multiplier)
        updated_params.append(global_params + grad_k_dp)
    
    return np.mean(updated_params, axis=0)

# Example usage
if __name__ == "__main__":
    # Suppose we have a global 2D model parameter vector
    w_global = np.zeros(2)
    
    # Example: 3 clients with synthetic data
    clients_data = [
        (np.array([[1, 2], [0, 1]]), np.array([1.0, 0.0])),    # (X, y)
        (np.array([[3, 2], [4, 1]]), np.array([2.0, 3.0])),
        (np.array([[10, 2], [8, 2]]), np.array([4.0, 5.0]))
    ]
    
    # Run a few rounds
    for t in range(5):
        w_global = federated_round(w_global, clients_data, clip_norm=2.0, noise_multiplier=0.5)
        print(f"Round {t}, global params = {w_global}")

This simple loop demonstrates the skeleton of a DP-based federated approach. For robust or encrypted aggregations, you would replace the relevant lines with calls to RFA or an HE library.

Conclusion

Federated learning offers a promising framework for training models on distributed, privacy-sensitive data. From the baseline FedAvg aggregator to advanced robust methods like geometric median, from differential privacy’s noise-based defense to full-blown homomorphic encryption, there are numerous paths to secure FL. In practical terms, each technique introduces extra complexity — computational overhead, accuracy trade-offs, or system-level engineering challenges. Nonetheless, the synergy of these approaches can yield a training pipeline that significantly curbs data leakage and malicious tampering.

If you’re curious about more details (especially from an academic standpoint), feel free to check out my bachelor thesis and code. The thesis also goes deeper into these approaches — covering the subtle interplay of security, memory usage, communication overhead, and performance in federated settings.

As you explore or implement FL solutions — be it in medical contexts, IoT, or any decentralized setting — knowing how to properly deploy robust aggregators, differential privacy, and encryption can be an invaluable shield for your users’ data.